Home and Learn: Microsoft Excel Course
Standard Deviation and Excel Bell Curves
Excel does have a Standard Deviation formula built in. But this article is to help you get a greater understanding of what it is and how it is calculated. You'll learn about the difference between the Population Standard Deviation and the Sample Standard Deviation. You'll also learn about the Normal Distribution, variance, and learn how to create a Bell Curve graph in Excel.
What is Standard Deviation?
Standard deviation is another way to measure the Central Tendency (Median, Mean, Mode, etc). It tells you how close or far away your values are from the mean (average). Let's see how it's calculated. It's not too scary!
Suppose we had a class of ten students. We gave them an exam and noted the scores out of 100. Let's say the scores were these (create this spreadsheet for yourself.):
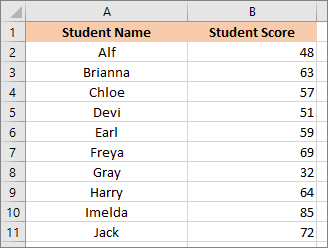
Looking at the table, we can see that the highest score was Imelda at 85, and the lowest score was Gray at 32.
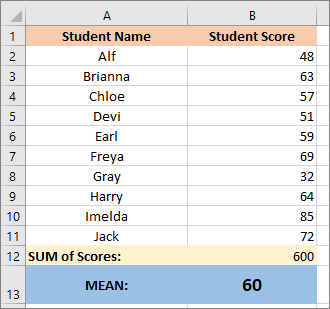
The Mean of these exam results is the sum of the scores divided by the number of students. So, add up all the scores in the B column and we get 600. There are 10 students. 600 divided by 10 gets us a Mean of 60:
Mean: 600 / 10 = 60
Let's enter that on our spreadsheet. In cell B12, enter:
=SUM(B2:B11)
And in cell B13 enter:
=Average(B2:B11)
The spreadsheet will look something like this:
You could go ahead and enter Excel's own standard deviation. It would be this:
=STDEV.P(B2:B11)
In statistics, a lowercase Greek letter sigma is used for standard deviation. So you'll often see this, as it's the symbol for standard deviation:
σ
There is an uppercase sigma, by the way. It is used to denote the Sum of. It's this:
Σ
Sample standard deviation formula versus Population standard deviation formula
Back to Excel. There's also a STDEV.S. The P stands for population and the S for sample. We're using the P version because we're assuming our 10 students are the entire population, that they are the only ones taking the test. If we had, say, 100 students then we would use the P for these 100, the entire population, and the S version for just a sample of these 100 students. We'd then have two different STDEV scores, one for the entire population and one for the sample. So, use STDEV.P if you're sure you're covering the entire population; use STDEV.S for your sample standard deviation formula.
But the number you'd get entering the STDEV.P formula would be 13.76. That would be where most of your scores would fall: 13.76 to the left of the mean of 60 and 13.76 to the right of it. So, all scores between about 36 to 74, which would be most of them. That 13.76 is one standard deviation from the mean of 60. Two standard deviations is about 28, if we round up, and three standard deviations is 56.
But how does Excel calculate all this? We're going to find out.
Deviation from the Mean
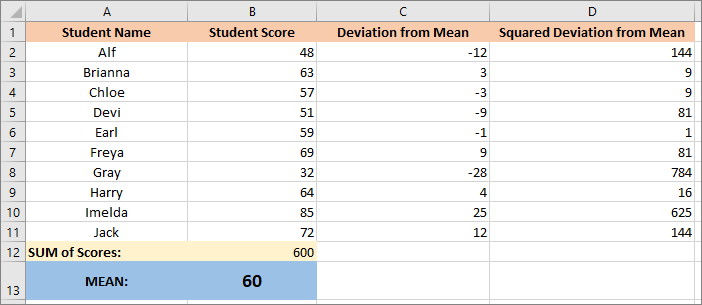
The first thing we need to do is to calculate how far each score deviates from our mean of 60. Alf at the top, for example, is 12 points below the average of 60. We need this, then, for each of the numbers in the B column:
Score - Mean
In Excel, we'll add a C column. Alf's deviation from the mean score will go in cell C2. The formula is then this for cell C2:
=B2 - B13
This gives Alf a mean deviation figure of -12. When all the other scores are calculated, we have this:

Before we can work out the what the standard deviation is, we need something called the Variance.
Variance
Variance is defined as, "The average of the sum of the squared mean differences". The Standard deviation is then the square root of the variance. Sounds complicated, but it's easy to see in practice. Let's get the squared mean differences first. This is just squaring the numbers we have in the C column on our spreadsheet. We do this to get rid of the negative numbers. So, Alf's deviation from the mean is -12. When we multiply -12 by itself (squaring) we get this:
Squared Deviation from Mean: -12 * -12 = 144
In Excel, the formula to enter in cell D2 for Alf is:
=C2 ^ 2.
Or you could use this instead:
=POWER(C2, 2)
The result is the same.
Enter one of those and then flood fill the rest.
Here's the spreadsheet now:
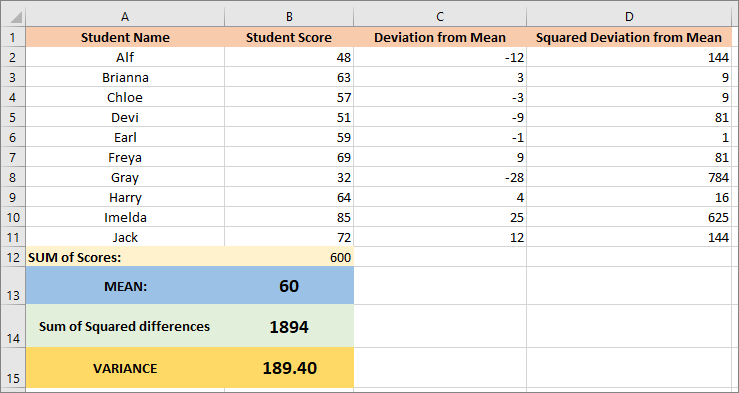
To get the average of these squared deviation numbers, add up all the values in the D column. Then divide by the number of students. This will give us the Variance.
In cell A14, enter: Sum of Squared Differences
In cell B14, enter the following formula:
=SUM(D2:D11)
In cell A15, enter the following text: Variance
Now enter this formula:
=B14 / COUNT(B2:B11)
Here's our spreadsheet now:
In statistics, a lowercase sigma is used for variance, along with the square symbol (superscript 2). So you'll often see this:
σ2
Standard Deviation
Only one more step to get the standard deviation.
Because the standard deviation is the square root of the variance, we can enter this in cell B16:
=SQRT(B15)
This gives us a figure of 13.76:
That's the figure we got from Excel's own standard deviation formula. And now you know how Excel works it out!
Here's a recap of what the figure of 13.76 means.
Remember, we're still measuring the central tendency. We started out with the mean of 60. One standard deviation from this central figure of 60 is 13.76 to the left of the centre line and 13.76 to the right of it. If we round up, this means one standard deviation is between 46 and 74:

Two standard deviations mean we double our 13.76 to 27.52. Again, round up to 28 and that will get us all scores between 32 and 88:

Three standard deviations take in all the scores between 18 and 102.
Most of your values will fall in the one standard deviation range. In fact, it's usually 68%. Two standard deviations will take care of 96% of your data, and three standard deviations will account for 99% of your data. So, in our sample size of 10 this means, if we round up from 6.8, we'll have 7 students in the 1 standard deviation range. (68% of 10.)
Now let's see how we can get one of those bell curve graphs.
Excel Bell Curve Graph
You can create a standard deviation graph. If your data has a normal distribution, you'll get the famous bell curve graph, like the one above.
Normal Distribution aka Gaussian Distribution
Distribution is a measure of how spread out your values are. When plotted on a graph, these values might gather more to the left or more to the right, or just be a complete mess. When your values are mostly grouped around the centre, it's said to have a Normal Distribution, like the bell curve in the images above. A Normal Distribution looks symmetrical when you plot your numbers on a graph.
To get a bell curve graph in Excel, you need to take one more step and create a column of Normal Distribution figures. The formula in Excel for the Normal Distribution is this:
=NORM.DIST(CELL_REF, MEAN, std_dev, cumulative)
So you need a cell reference, a mean value, the standard deviation, and something called a cumulative option. For this last one, cumulative, you can just enter 0. This gets you the probability density function. If you entered 1, the only other value allowed, you'd get the cumulative distribution function and your graph would look weird.
In cell E2 on your spreadsheet, enter the following:
=NORM.DIST(B2, $B$13, $B$16, 0)
Press Enter then flood fill the rest of the column, down to E11,
You now need to sort the data. So, select the cells from A2 to E11. On the Home ribbon, locate the Editing panel. On the Editing tab, click on Sort & Filter, then on Custom Sort. In the Sort by dropdown box, select the B column where your scores are:
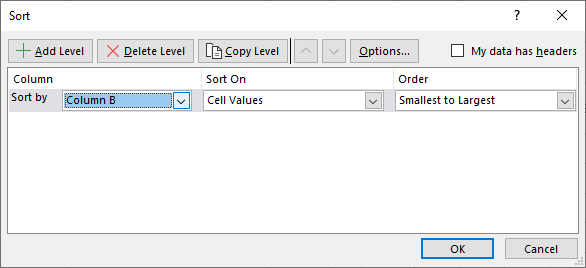
Click OK to sort your data. (If you don't sort the values, your chart will look odd.)
Your spreadsheet will look like this:
Time to select the data for the chart. This is the Student Scores and the Normal Distribution column. Select these two columns. (Select one column as per usual then hold down a CTRL key to select a second column.)
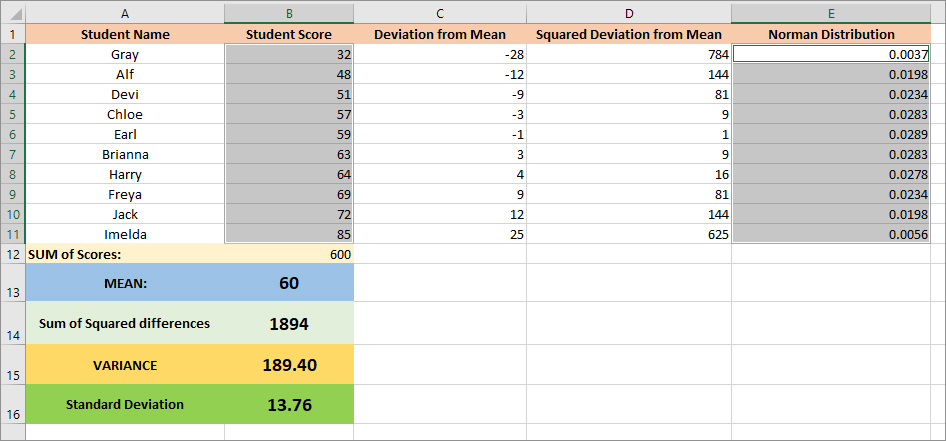
With the two columns selected, click on the Insert ribbon at the top of Excel. On the Charts panel, select the X Y Scatter Chart type:
Then click on the second one, Smooth Lines:
You should then have a chart like this on your spreadsheet:

Notice that this example doesn't produce the classic Bell Curve you may have seen elsewhere. This is because we don't have enough data. We only have 10 students. If we were to add lots more, with low and high scores in the mix, the curves at the bottom would start to flatten out to the left and right. Note also that our chart starts just after the 30 mark. This is because 32 is our lowest score. But you can still see that most of the score are between 46 and 74. (The 60 in the chart above is our Mean value.)
And that's it for this lesson on Standard Deviation. Hope you understand it now! In the next lesson below, we'll explore something closely related to standard deviation - Standard Error.
<--Back to the Excel Contents Page