Home and Learn: Android Course
Android Simple List - the Java Code
Open up your MainActivity.java file. We'll set up a couple of variables first.
Just after public class MainActivity and before the onCreate method, add these two variables:
ListView theListView;
Intent myIntent;
If you get any red text, press ALT + ENTER to add the correct libraries. Or add these two import statements at the top of your code:
import android.content.Intent;
import android.widget.ListView;
Your code window will then look something like this:

(The reason we're setting up these two variables at the top is because they need to be seen outside of the onCreate method a little later.)
The next thing we can do is get a reference to our ListView on the Activity. Add the following line to the onCreate method, just below setContentView:
theListView = (ListView) findViewById(R.id.myListView);
As usual, we use findViewById to get a reference to a view on a layout. The ID this time is myListView, which is what we renamed our ListView to.
Next, we can set up a String array. The array will be used to fill the ListView. (if you're not too sure about arrays, see this page on our Java course: Java Arrays )
Add this line below the previous one:
String[ ] myData = {"Visual Basic .NET", "Java", "Android", "C# .NET", "PHP", "C++", "Scala", "Ruby on Rails", "Javascript", "HTML", "Python", "Swift"};
This sets up a String array with the name myData. You can change the items in the array to anything you like. But each item will be used to fill up a place on the ListView when the app starts up. So Visual Basic .NET will be at the top of the list, Java will come second, followed by Android, etc.
Your code so far should look like this:

Now that we have reference to the ListView and have set up an array for the list, the next thing to do is to set up something called an ArrayAdapter.
An ArrayAdapter acts as a kind of assistant to help the Activity, the ListView and the data team up with each other. They can be slightly awkward to set up. They look like this:
ArrayAdapter<String> myAdapter = new ArrayAdapter<String>( PARAMETERS_HERE );
You start with the word ArrayAdapter. In between pointy brackets, you need the type of data that is going in to the adapter , String in our case. You then type a variable name for your ArrayAdapter. We've called ours myAdapter. After an equal sign, we then have this:
new ArrayAdapter<String>( PARAMETERS_HERE )
We're trying to create a new ArrayAdapter object here. After ArrayAdapter<String> comes a pair of round brackets:
ArrayAdapter<String>( )
The round brackets are for the class constructor (there are six constructors in all). In between the round brackets, you can choose from up to from up to four different parameters. We only need three:
Context
Resource
List
The Resource one is a layout. We don't need to create this layout ourselves as there's an inbuilt one we can use.
So, add this line to your code:
ArrayAdapter<String> myAdapter = new ArrayAdapter<String>( this, android.R.layout.simple_list_item_1, myData );
The keyword this means this particular context (Activity). After a comma, we have this:
android.R.layout.simple_list_item_1
When you type a dot after android.R.layout, you'll see this list appear:

As you can see, there are quite a lot of items to choose from. The one we want is called simple_list_item_1. This gets you a single TextView for each item in your list.
After a final comma, we have the name of out String array, which was myData:
ArrayAdapter<String>( this, android.R.layout.simple_list_item_1, myData );
Your code should look like this (we've spread our ArrayAdapter over two lines):
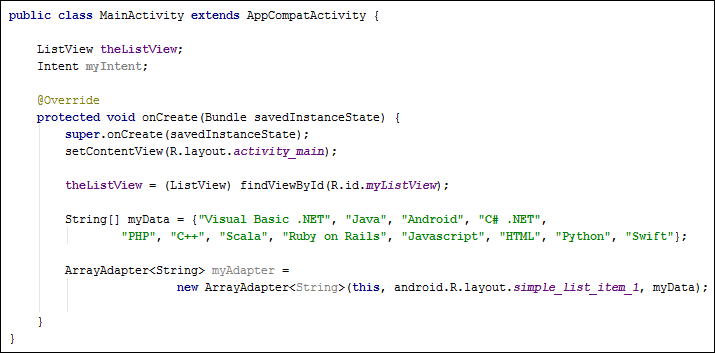
One more line to add before you can try it.
Once you have set up your adapter, you need to attach it to your ListView. Ours was called theListView, which we set up at the top of the code. Add this line, then, below your ArrayAdapter:
theListView.setAdapter( myAdapter );
The inbuilt method we can use is called setAdapter. In between the round brackets of setAdapter, you type the name of your ArrayAdapter, myAdapter for us.
Try it out. Run your app and see what happens. If all went well, you should see this:

If you select an item on the list, however, nothing happens. We'll write code to fix that now.
< Simple Lists| ListView Item Selection >
Back to the Android Contents Page